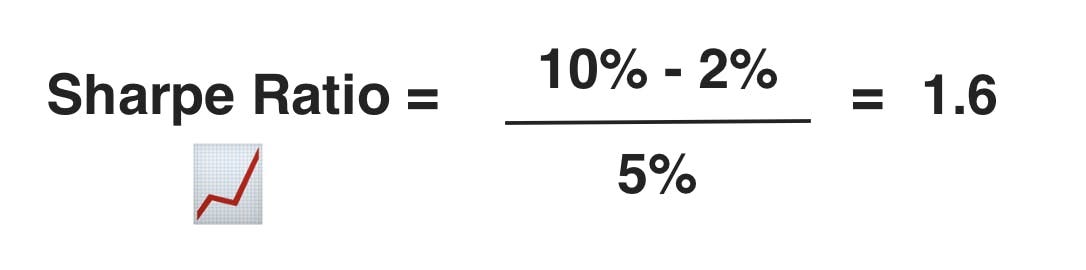💡 What is Risk-Adjusted Return?
Issue 116
✌️ Welcome to the latest issue of The Informationist, the newsletter that makes you smarter in just a few minutes each week.
🙌 The Informationist takes one current event or complicated concept and simplifies it for you in bullet points and easy to understand text.
🫶 If this email was forwarded to you, then you have awesome friends, click below to join!
👉 And you can always check out the archives to read more of The Informationist.
Today's Bullets:
What is Risk Adjusted Return?
The Sharpe Ratio
Investment Examples
Inspirational Tweet:
When you hear long-time investors speak about assets, securities, and their returns, you inevitably hear something known as 'risk-adjusted returns', especially when discussing volatile investments.
Especially volatile assets, like Bitcoin. Though, volatility has often been called a feature of Bitcoin. Not a bug.
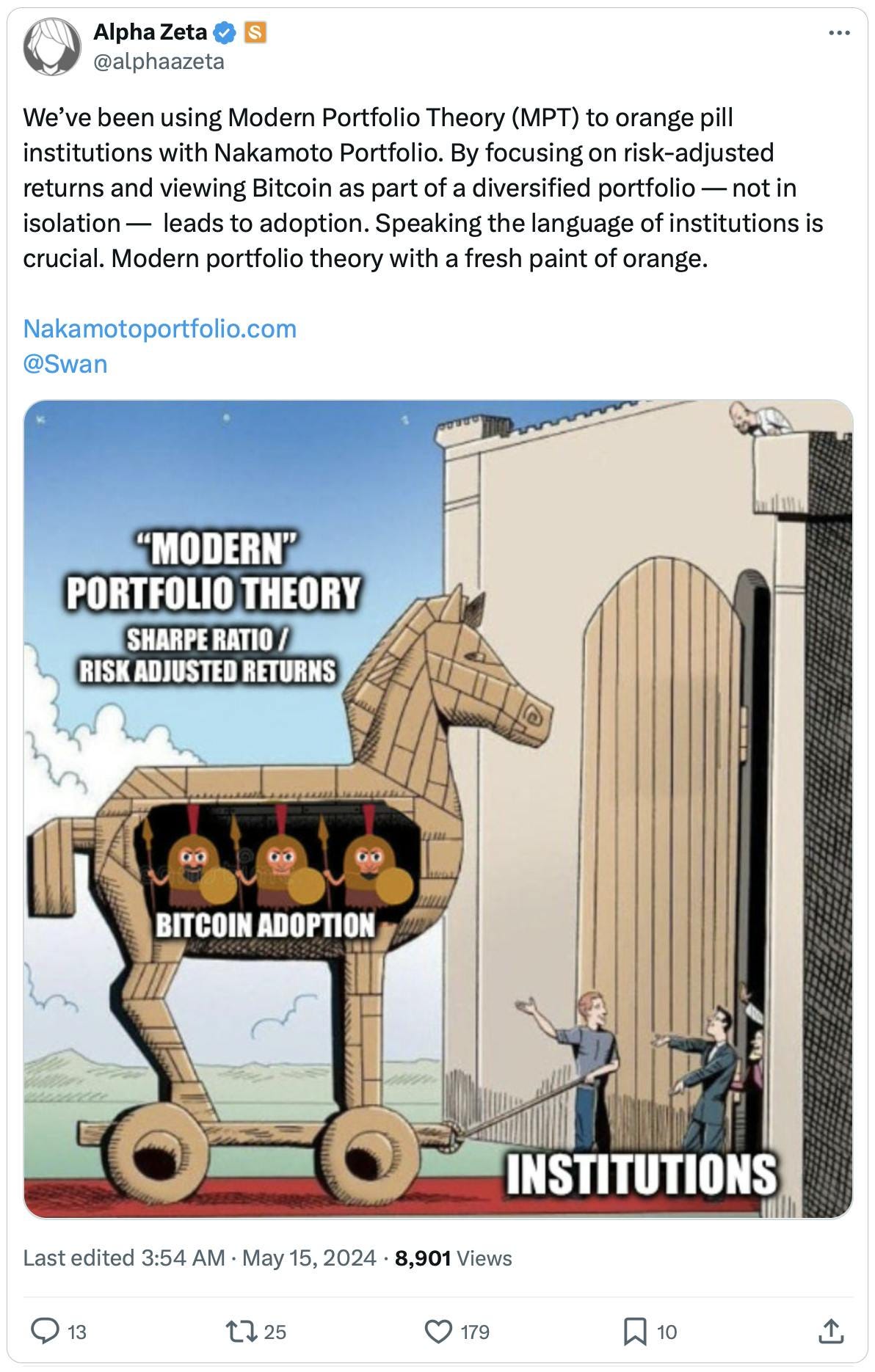
And so, as my friend Rapha Zagury (@alphaazeta on Twitter/X) astutely points out, risk-adjusted returns are a critical part of communication when meeting with institutional investors, regardless of the asset or strategy being discussed.
But why are institutions and professional investors so fixated on this measure.
I mean, what exactly is risk-adjusted return, and does it really matter?
If you have no idea what the answers to these questions are, don't worry, you're about to know exactly what Rapha is talking about and why it is indeed so important when looking at and deciding between investments.
But have no fear, because we do things nice and easy around here, keeping it simple and straight to the point.
So, grab a cup of coffee and settle in, as we explore risk and return with The Informationist today.
🤠 What is Risk Adjusted Return?
Put simply, risk-adjusted return (RaR) is a measure that evaluates the return of an investment relative to the risk taken to achieve that return.
Returns can be expressed as the price of the investment rising (capital gains), and dividend or interest paid by the investment.
Risk refers to the possibility that the actual return on an investment will differ from the expected return. And so, risk is often measured in terms of volatility or what is known as standard deviation.
Don't worry, we'll cover that in a moment.
Bottom line, risk measures uncertainty.
The point of measuring this risk is to level the playing field by incorporating both potential rewards and associated risks of various investments.
Why do we do this as professional investors?
Simple.
RaR gives us a way to compare different investments, even if they have different levels of risk. In other words, a high-risk, high-return investment can be directly compared with a low-risk, low-return investment to determine which one offers better returns relative to its risk.
If this has you thinking US Treasuries versus Bitcoin, for example, stay tuned.
And the ultimate reason investors want these RaR measures is to help them build a portfolio that maximizes returns while attempting to minimize risk.
This is exactly where standard deviation comes in.
What is Standard Deviation?
Standard deviation measures how much an investment’s returns vary from its average return.
In this way, standard deviation shows how spread out the returns are. Higherstandard deviation means more variability (riskier), while lower standard deviation means less variability (safer).
We won't get into the math of it all here, but suffice to say, standard deviation is a calculation of returns and averages that produces a number to show this variance.
And so, if Investment A has a standard deviation of 5% and Investment B has 10%, Investment B is deemed to be riskier.
But this is only part of the equation.
The second part of the equation has to do with the actual returns of each investment.
What if Investment A has a 3% annual return, but B has a 5% return.
Which investment has a better risk-adjusted return?
I mean, B is more volatile, but with higher returns, and A is less volatile, but lower returns.
This is where a number of other risk measures come into play.
There are numerous risk and RaR measures that professionals like to use, such as: Value at Risk (VaR), Information Ratio, Sortino Ration, Treynor Ratio, Omega Ratio, Jenson's Alpha, Sharpe Ratio, and more.
A hedge fund staple and institutional investor favorite is the Sharpe Ratio.
So, let's key in on that one for today, and see how it can help us determine the RaR of an investment.
🤓 The Sharpe Ratio
In short, the Sharpe Ratio uses standard deviation to help investors understand how much excess return they are receiving for the extra volatility they endure by holding a riskier asset.
Sharpe Ratio Formula
WAIT. Don't panic.
It's not really that complicated, just a bunch simple concepts and measures:
Return is the average return of the investment over a determined time period
Risk-Free Return is the risk-free rate for the same period, and is usually quoted as a government bond (I know, there is no such thing as 'risk-free', but for the purposes of this exercise...😏)
Standard Deviation is just that, the standard deviation of the investment
Example
Suppose we have the following data for an investment:
Average Return: 10%
Risk-Free Rate: 2%
Standard Deviation: 5%
Using the formula:
This means the investment provides 1.6 units of excess return for each unit of risk (standard deviation).
And so, a higher Sharpe Ratio indicates a better risk-adjusted return, as it means the investment is providing more return per unit of risk.
And vice-versa for a lower Sharpe Ratio.
For reference, a good Sharpe Ratio has historically been considered to be above 1.0. This has been a challenge recently, of course, with the tremendous volatility in the markets over the last number of years.
Even so, using the Sharpe Ratio, let's look at the risk adjusted returns of various investments.
🤑 Investment Examples
Let's compare a few different assets based on their risk-adjusted returns (RaR)over the last 10 years.
We will use:
TLT: iShares 20+ Year Treasury Bond ETF to represent US Treasuries
SPY: SPDR S&P 500 ETF Trust to represent stocks
GLD: SPDR Gold Trust for Gold
and Bitcoin
And here are the results, as computed by the Nakamoto Portfolio website (created by Rapha Zagury):
*note, these are results on just under 10 years of data*
So what do we see, and what can we learn from this?
A few things.
First, even though the US Treasury is supposed to be a 'risk-free asset', the TLT has displayed tremendous volatility in the last 10 years. More volatility than Gold, in fact. 😮
Second, the returns of long bonds were just dismal. And when inflation adjusted, they are actually negative real returns.
This is why the TLT has the worst Sharpe Ratio, and is hence the worst risk-adjusted return of the assets listed here.
You can chalk this up to relentless central bank manipulation of the money supply and rates, but regardless, not good.
Next, we notice that the annual volatility of Bitcoin is massive, almost heart-attack inducing to some, perhaps. 😱
No surprise.
That said, look at the returns of Bitcoin over the last ten years. A whopping 14 thousand percent!
Simply blows the field away.
And THIS is why it earns the highest risk-adjusted return here, nearing that coveted 1.0 score.
Putting it all together:
Bonds (TLT):
Annualized Return: 0.29%
Sharpe Ratio: -0.08
With low returns and high volatility, the negative Sharpe Ratio indicates that the returns have not been sufficient to compensate for the risk taken, making it a less attractive option for risk-adjusted performance.
Stocks (SPY):
Annualized Return: 12.56%
Sharpe Ratio: 0.62
The S&P 500 (SPY) has delivered strong annualized returns with a decentSharpe Ratio over the last decade. This reflects a favorable balance between return and risk, making SPY an attractive option for long-term growth-oriented investors.
Gold (GLD):
Annualized Return: 6.6%
Sharpe Ratio: 0.35
Gold has historically been viewed as a safe-haven asset, but its returns over the past decade have been pretty modest. The low Sharpe Ratio indicates that the returns have not sufficiently compensated for the associated risk. That said, Gold is often uncorrelated to other asset classes, making it a solid addition to most portfolios.
Bitcoin
Annualized Return: 67.01%
Sharpe Ratio: 0.93
Although it has significant volatility, Bitcoin has delivered exceptionally high returns over the past decade. The Sharpe Ratio of 0.9, even higher than stocks, suggests that Bitcoin offers substantial risk-adjusted returns.
But let's be clear. The Sharpe Ratio is one measure of many, and in reality there are a number of other calculations and ratios that professional investors are looking at when making decisions on investing in any one asset or security, as well as building a portfolio of them.
That said, when looking at the risk adjusted returns of Bitcoin, in particular, it seems that volatility is, in fact, a feature, and not a bug.
And so, even though it has only been around for 15 years, with the new spot-ETFs and easy onboarding of institutional investors that has only just begun, I personally expect this adoption and price appreciation to continue.
Taking this all to the next level, we would then look at the effects of adding each of these assets to a portfolio at various weights and with various parameters. We would look at Sharpe Ratios of those portfolios against each other and make security (or asset) selection and weightings decisions, accordingly.
That, however, is a whole 'nother discussion. One that would require a full newsletter to dissect.
Perhaps soon...
That’s it. I hope you feel a little bit smarter knowing about risk adjusted returns and the Sharpe Ratio after today.
If you enjoy The Informationist and find it helpful, please share it with someone who you think will love it, too!
Talk soon,
James✌️